Project 4: Image Mosaicing
In this project, we initially took many photos, each set containing a significant portion that overlaps with others. We can use these overlapping sections to stitch the photos together, forming a larger image. To achieve this, we need to first identify the corresponding points between these photos and then perform projection warping. We can use this warping technique for other purposes, such as image rectification, which projects an object that is not facing forward in the photo to appear as if it is facing forward, allowing us to view the object from different angles. Afterwards, we can also use blending to combine many photos into one larger image.
Part A: Manual Feature Selection and Image Mosaicing
In this part, we implement image mosaicing using manual feature selection to understand the fundamental concepts of homography and image warping.
Part A1: Shoot the Pictures
First, I took these sets of photos simultaneously. I also made sure to keep the center of projection (COP) fixed, which ensures that the transforms between them are projective. Additionally, each set of photos has a large overlapping area, allowing us to use these overlapping sections to stitch the photos together and form a larger image.
These are the photos I took in my apartment:


These are the photos of the Bay St Mall:


These are the photos I took in the hallway:


Part A2: Recover Homographies
Before implementing warping, we need to first identify corresponding points between the images. Since there are many overlapping areas in the two pictures, I found objects that appear in both images and used the tool from Project 3 to mark their corresponding points.



Before warping, we need to recover the parameters of the transformation between each pair of images. Our transformation here is a homography: \( p' = Hp \), where \( H \) is a 3x3 matrix with 8 degrees of freedom (scaling factor set to 1). According to the formula from Lecture 11, slide 42: \[ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} \] As long as we have more than 8 \((x,y,x',y')\) point pairs, we can solve for \(H\), like this: \[ \begin{align*} &\begin{cases} ax + by + c = wx' \\ dx + ey + f = wy' \\ gx + hy + 1 = w \end{cases} \\ \implies &\begin{cases} ax + by + c - gxx' - hyx' = x' \\ dx + ey + f - gxy' - hyy' = y' \end{cases} \\ \implies &\begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -xx' & -yx' \\ 0 & 0 & 0 & x & y & 1 & -xy' & -yy' \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix} \end{align*} \] Specifically, we stack all the \((x,y,x',y')\) point pairs into matrix \(A\) layer by layer, and stack all the \(x'\) and \(y'\) into matrix \(B\) layer by layer. Then we used `np.linalg.lstsq` to solve this linear equation system to get the least squares solution. Reshape this solution into a 3x3 matrix, and that's our \(H\).
Part A3: Warp the Images
After calculating the homographies, we utilize them to warp the images effectively. Specifically, we use the homography matrix 𝐻 to re-project one image onto the canvas of another. This process involves creating a coordinate grid for the destination image and then transforming each coordinate through the homography to find the corresponding points in the source image. Bilinear interpolation is then applied to fill in the pixel values in the destination image. Here's how this works in practice: Initially, we determine the bounding box of the final image by applying the homography to the four corners of the first image to project it onto the second. This outlines the area where the final image will reside. We then use scipy.interpolate.RegularGridInterpolator to interpolate the pixel values from the source image and map them onto the destination image. Because the coordinates after warping may be negative, we will shift this grid to ensure all coordinates are positive. Also, we can use this shift for alignment later.


Part A4: Image Rectification
Using the same method, we can achieve Image Rectification. First, I took several photos that contain rectangular objects, but they are not necessarily rectangular in the photos. First, we still need to mark the rectangular objects in these photos. I marked four points on each rectangular object, but since we only have one photo and we just want to rectify it, the corresponding points for the second image are designed by myself, such as (0,0), (0,1), (1,0), and (1,1). Then, using the method described above, we calculate the homography matrix and perform the warp. This way, we can rectify any image or view the object from different angles.


Part A5: Crafting the Image Mosaic
After warping the images, we can blend them into a mosaic. Specifically, we can use the homography matrix to warp the images onto a canvas of another image, and then we can use the shift to align the images. After warping, we can use the blending technique to combine the images into one larger image. Here's how we can do this:
- Warping and Aligning: We begin by applying a homography matrix to the first image to warp it appropriately. This results in a transformed image and an alpha mask. We also track how much we need to shift this image to align perfectly with the second image.
- Determining Mosaic Dimensions: Next, we calculate the dimensions needed for the mosaic canvas to ensure that it can accommodate both images fully without any clipping.
- Image Placement: Each image is positioned on its designated canvas. Adjustments based on previously calculated shifts are made to align them perfectly.
- Distance Transformation: A Euclidean distance transform is applied to both masks. This transform measures the distance of each pixel to the nearest boundary, influencing the blending behavior by giving less weight to boundary pixels.
- Two-band Blending: The images undergo a blurring process to separate high and low-frequency details. Low-resolution components are blended using weighted averaging based on the alpha masks (we use distance transformation as the alpha mask). High-resolution components are blended using a decision-based approach where pixels from the image with the higher distance transform value at each location are chosen.
These are the results of the mosaic:







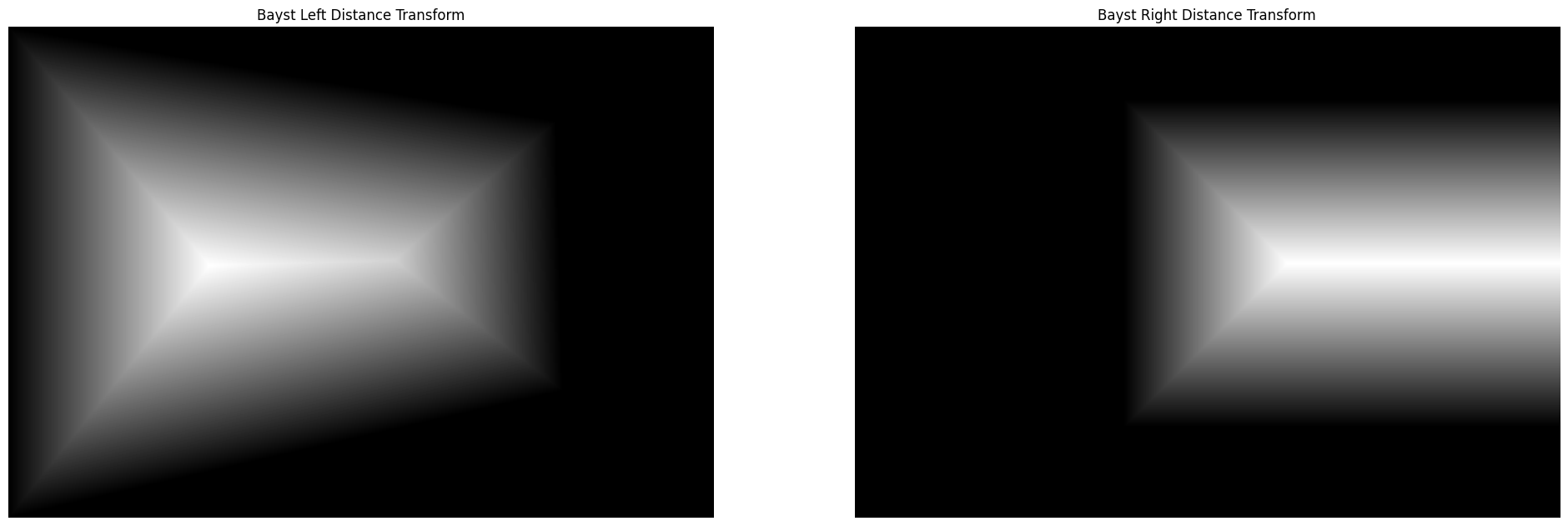


These are the photos I took in the hallway:


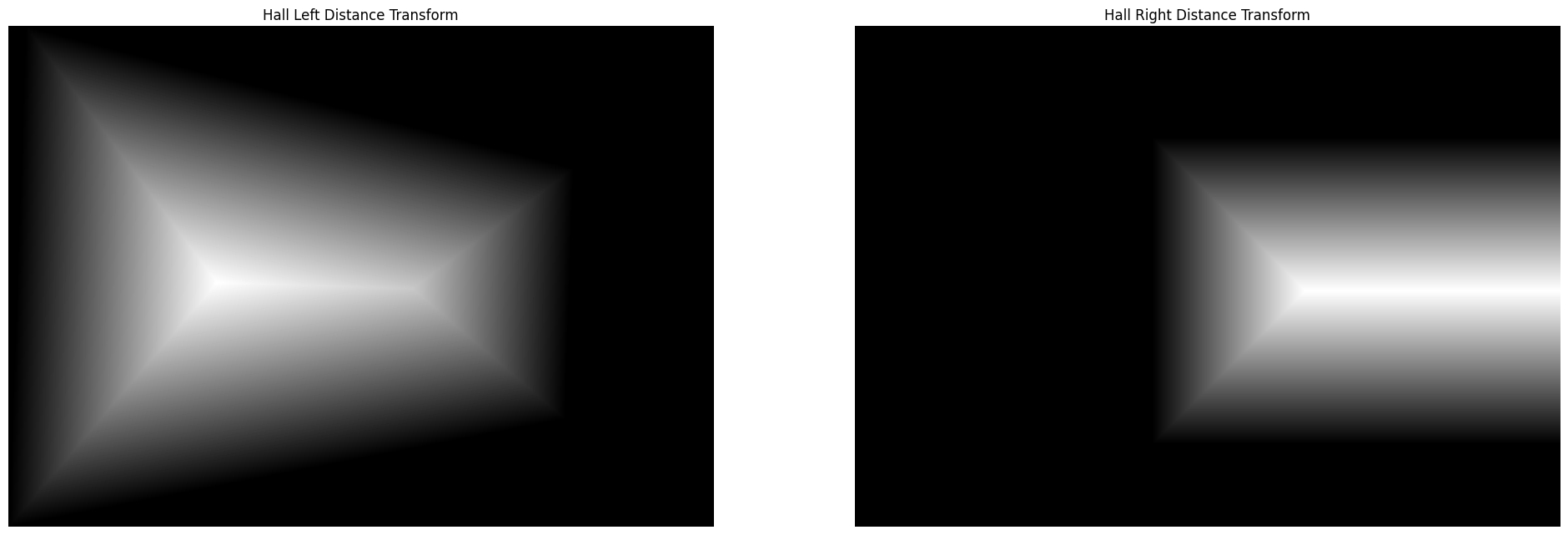


Part B: Automatic Feature Detection and Matching
In this part, we implement automatic feature detection and matching to create image mosaics without manual point selection.
Part B1: Harris Interest Point Detector
Firstly, in order to find the interest points, we would like to focus on the "corners" of the image. To find these corners, we use the Harris interest point detector, which identifies points where the image has strong gradients in multiple directions. Using the implementation from harris.py, we set σ=1 for the Gaussian smoothing and min_distance=1 to make the detected peaks to be at least one pixel apart. The function returns both the Harris response values (h-values) for each pixel and the coordinates of detected interest points. These points represent locations in the image where there are significant changes in intensity in multiple directions, making them good candidates for feature matching. Here is the Harris Matrix and the detected interest points for one of the images:


Number of Harris corners: 11607(Left), 11583(Right)
Part B2: Adaptive Non-Maximum Suppression (ANMS)
After applying the Harris corner detector, we often get too many interest points that are heavily clustered. This clustering can be problematic as it provides redundant information and doesn't give us a good spatial distribution of features across the image. To address this, we implement Adaptive Non-Maximum Suppression (ANMS) based on the Multi-Image Matching using Multi-Scale Oriented Patches paper.
The ANMS algorithm works as follows:
- For each interest point p, we find its "suppression radius" r, which is:
- The minimum distance to any other point q where H(q) > c_robust * H(p)
- Here, H(p) is the Harris response at point p
- c_robust (set to 0.9) helps ensure robustness to noise
- We use a k-d tree data structure to efficiently find nearby points within a radius of 24 pixels
- Points with larger suppression radii are better because they are far from stronger interest points
- Finally, we select the top 100 points with the largest suppression radii
This approach ensures that:
- Selected points are well-distributed across the image
- We maintain only the strongest interest points in any local region
- The final set of points is more suitable for feature matching

Number of Interest Points After ANMS: 100
Part B3: Feature Descriptor Extraction
For each interest point, we extract a feature descriptor that captures the local image appearance according to the paper. We only consider the axis-aligned features according to the instructions. The process is as follows:
- Extract a 40×40 pixel patch centered at each interest point
- Apply Gaussian blur (σ=2) to avoid aliasing
- Subsample to 8×8 patches (spacing = 5 pixels)
- Normalize and flatten the descriptor (μ=0, σ=1):
- Subtract mean
- Divide by standard deviation

Part B4: Feature Matching
With features extracted, the next step is to match features together between two images to form correspondences. Our matching process uses several techniques to ensure accuracy:
- Distance Computation:
- Compute pairwise distances between all feature descriptors from both images
- Create two distance matrices for bidirectional matching
- Outlier Reduction:
- Apply Lowe's ratio test: for each feature, find its two closest matches and compare their distances
- Only accept matches where closest/second-closest distance ratio is below 0.8
- Implement cross-checking: ensure matches are reciprocal between both images
Below is an illustration of the feature matching results. The visualization shows matches between the two images, with red points in the left image connected to corresponding blue points in the right image via green lines. Each line represents a match that passed both the ratio test and cross-checking criteria.
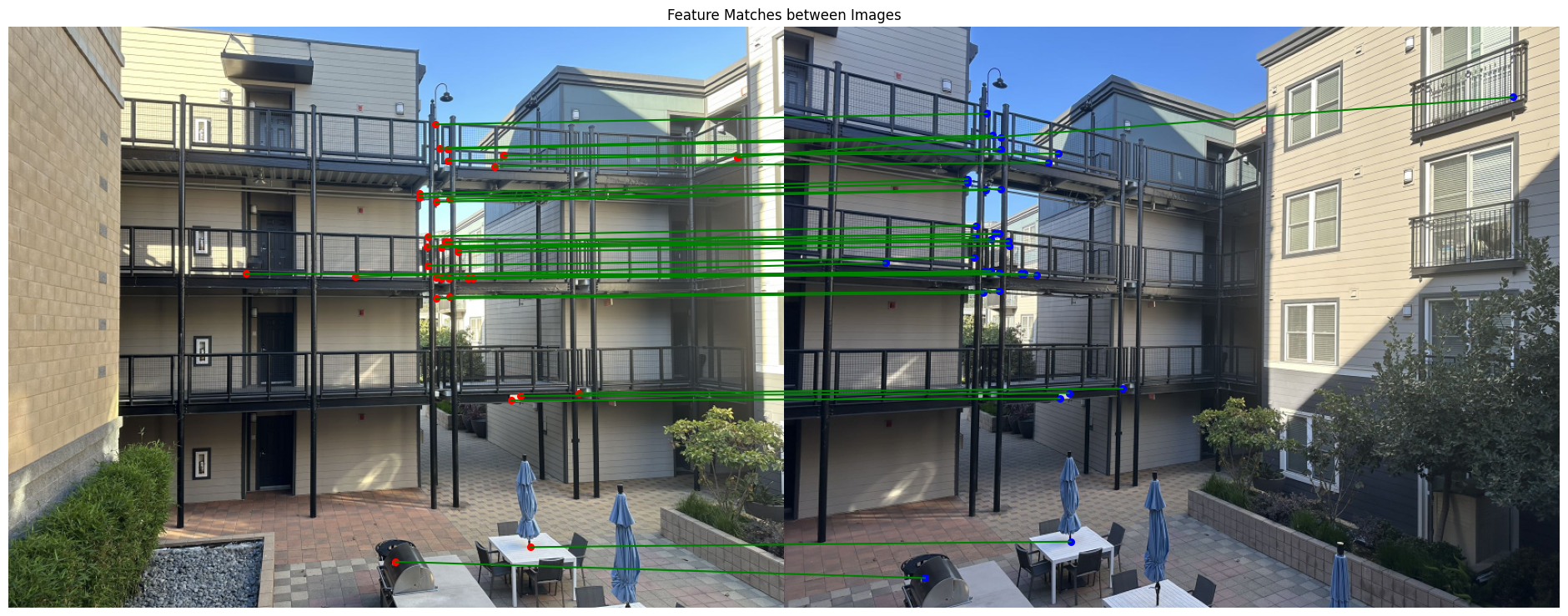
Feature matching with ratio threshold = 0.8
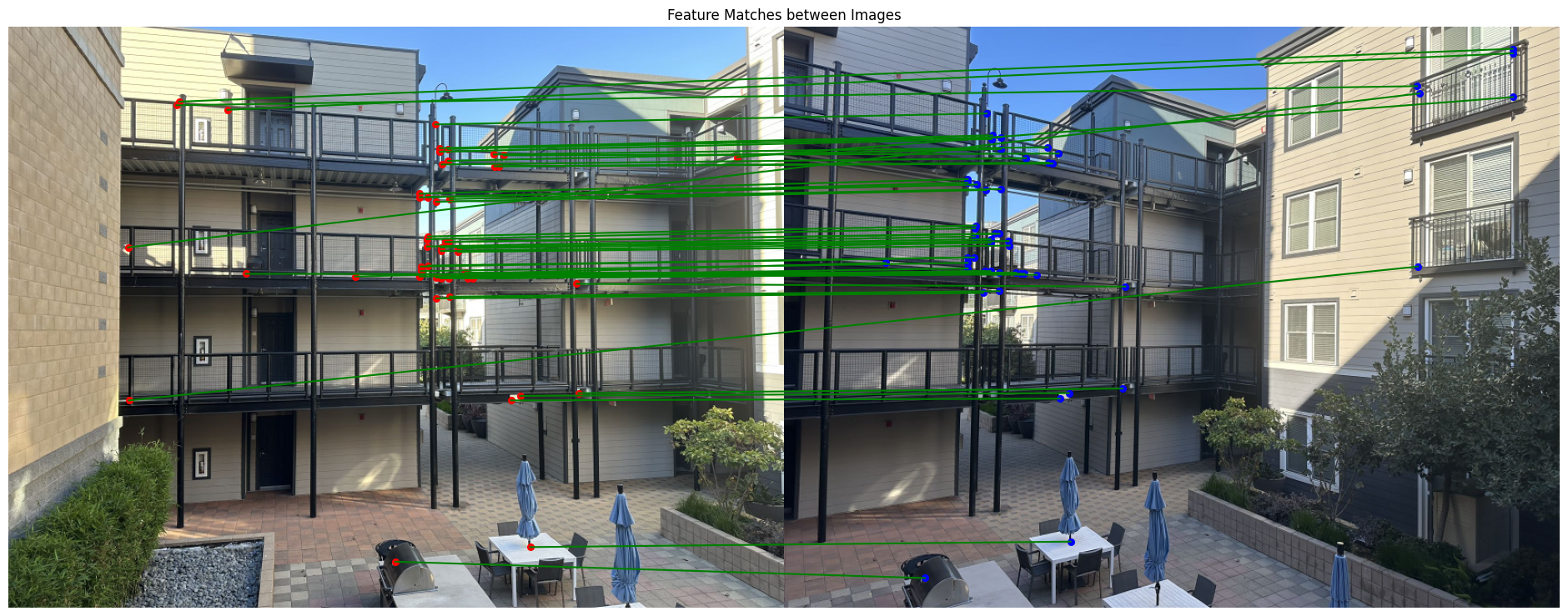
Feature matching with ratio threshold = 1
We can see that when the ratio threshold is larger, we get more matches, but also more outliers and incorrect matches. So I choose the ratio threshold = 0.8 for the rest of the experiments.
Part B5: RANSAC
While Lowe's ratio test helps filter out many incorrect matches, some mismatched pairs typically remain. These incorrect correspondences pose a significant problem because the least-squares method is sensitive to outliers - even a few incorrect matches can significantly distort the computed homography matrix.
To solve this issue, we implement RANSAC (Random Sample Consensus), an iterative method that works by repeatedly selecting small random subsets of matches (size of 4) to compute potential homographies. For each iteration, we track how many other point pairs align well with the current transformation (determined based on whether the difference in distance is below a certain threshold). Through many iterations, we identify the homography that best explains the majority of the matches, effectively filtering out the outlier pairs that don't fit the dominant geometric relationship between the images.
The RANSAC algorithm implementation involves:
- Randomly selecting 4 matching pairs
- Computing homography H from these pairs
- Transforming all points using H and counting inliers (points with transformation error < threshold)
- Repeating for many iterations (2,000,000 in our implementation)
- Keeping the H that produces the most inliers
The visualizations below show the matches that RANSAC identified as reliable. The red points in the left image are connected to their matching blue points in the right image via green lines. These connections represent the inlier matches that RANSAC determined were consistent with the best-fitting homography transformation. And the red lines are the incorrect matches that RANSAC filtered out.
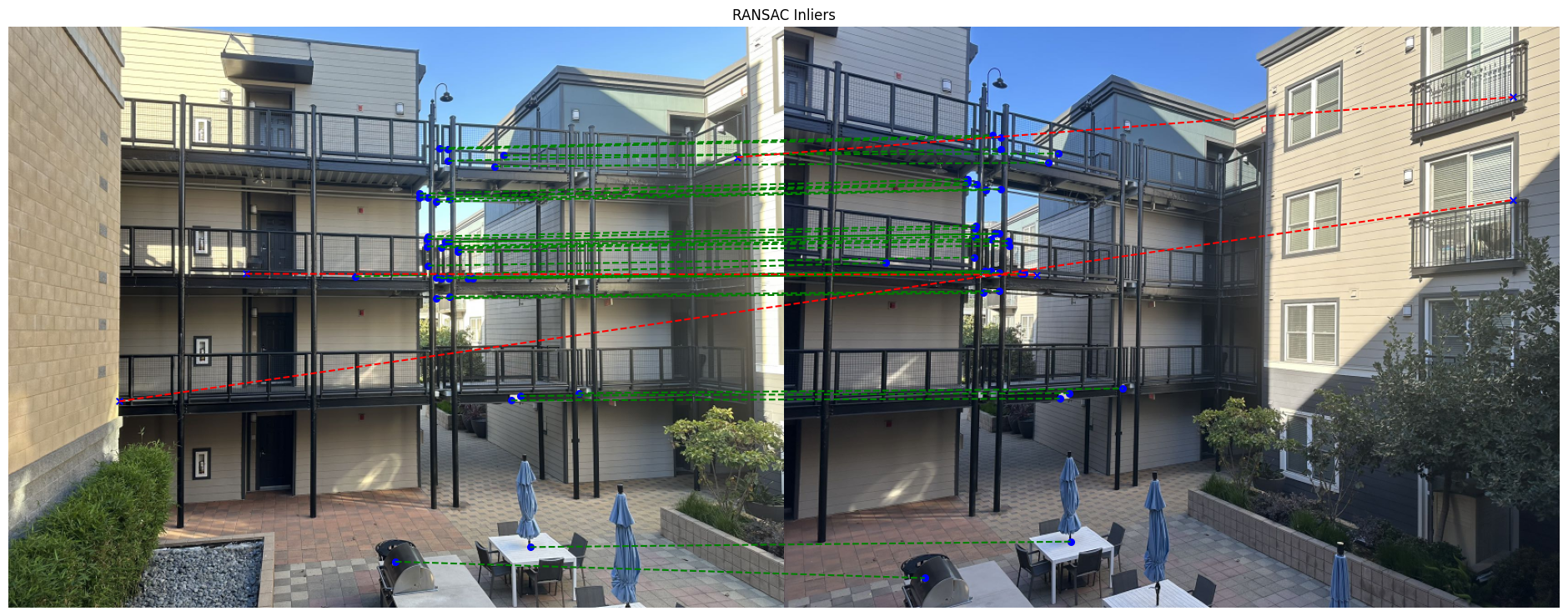
RANSAC results with threshold = 5
Part B6: Results
Using the automated feature detection and matching pipeline, we can create image mosaics without manual point selection. Below are the results for each photo set:
Apartment Photo Set

Original Left Image

Original Right Image

RANSAC Results
.png)
Apartment Final Mosaic (Automatic)

Apartment Final Mosaic (Manual)
Bay Street Photo Set

Original Left Image

Original Right Image

RANSAC Results
.png)
Bay Street Final Mosaic (Automatic)

Bay Street Final Mosaic (Manual)
Hallway Photo Set

Original Left Image

Original Right Image

RANSAC Results
.png)
Hall Final Mosaic (Automatic)

Hall Final Mosaic (Manual)
We can take any images that have the same COP and use the same pipeline to create a mosaic for them. I just took the photos of my desk and created a mosaic for them automatically.

Desk RANSAC Results
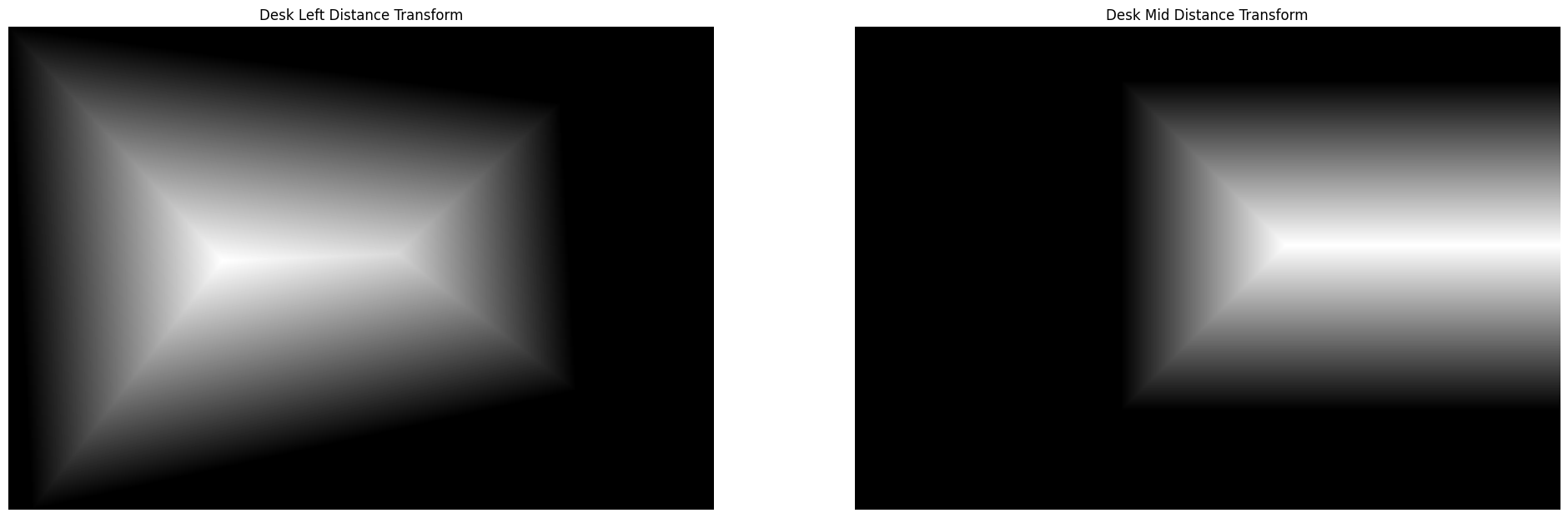
Desk Transform

Desk High Resolution and Low Resolution
.png)
Desk Final Mosaic (Automatic)